Spaghetti Trigonometry
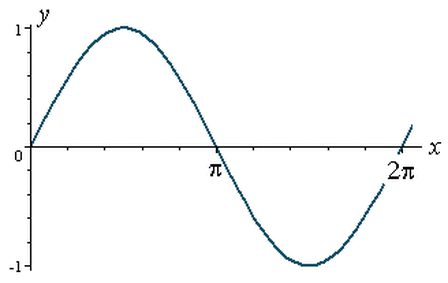
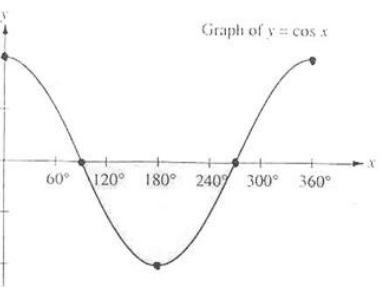
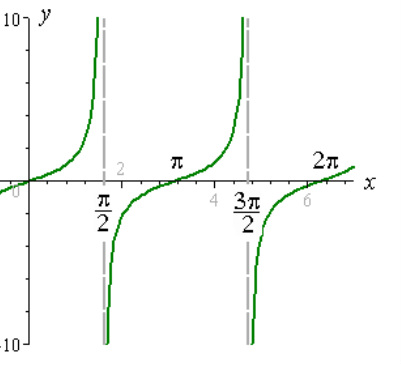
My partner and I began this project by creating a circle with a radius of one spagehtti noodle. Then, next to the circle we created a graph only showing quadrants one and four; the graph next to the circle is labeld every fifteen degrees. On the circle I then began drawing triangles at every fifteen degree mark where the radius is the ajacent side of the certain angle.From this I graphed the sine curve y=sin x with the period 2πr. After that, I graphed the functions of y=cos x with a period 2π and y= tan x with a period of π. The pictures shows the graphs of y=sin x, y-cos x, and y=tan x. These are the three problems that I graphed. Attached below is a PDF file of some questions on the graph of y=sinx.
| Speghetti Trigonometry Questions |
This is the curve of the sine; y=sinx.
This is the curve of cosine; y=cosx.
These are the tangent curves; y=tanx.
Skills and Objectives
Apply the Laws of Sine and Cosine to real-world
problems
Understand characteristics of y = sin x and y = cos
x
Graph sine functions
Apply properties of a unit circle to the
graphs
Solve a triangle using the Law of Sines
Find the area of a
triangle
problems
Understand characteristics of y = sin x and y = cos
x
Graph sine functions
Apply properties of a unit circle to the
graphs
Solve a triangle using the Law of Sines
Find the area of a
triangle
Justification
I chose to use this in my portfolio because it shows how I used my knowledge of trigonometry to create my own sine, cosine, and tangent curves.
